Modellierung
| Inhaltsverzeichnis: |
|---|
| Modellierung beschreibt den Prozess der Modellbildung und wird vorrangig im mathematisch-naturwissenschaftlichen Unterrichtsgeschehen verwendet. Dabei werden Fragestellungen des Alltags so aufgearbeitet, dass ein Modell entsteht, das unter Einbezug mathematischer Werkzeuge so bearbeitet werden kann, dass wiederum für die Realität relevante Ergebnisse erzielt werden können. Die gängigste Art der Beschreibung der Modellierung ist eine entsprechende Kreislaufdarstellung. |
| Tatsächlich lässt sich der Begriff Modellierung nicht exakt scharf von anderen offenen Aufgaben abgrenzen und eine Definition muss entsprechend weit gefasst werden. Den Versuch einer Definition liefert Katja Maaß: „Zunächst muss man eine Situation als mathematikhaltig erkennen und kann dann eine entsprechende Frage formulieren. Nun sind mehr oder weniger komplexe Sachverhalte zu vereinfachen und zu mathematisieren, bevor man das Problem mit mathematischen ‚Werkzeugen‘ bearbeiten kann. Ist schließlich eine Antwort gefunden, stellt sich die Frage, ob sie wirklich eine gute Lösung für das Ausgangsproblem darstellt.“ (Maaß 2007, S.7)
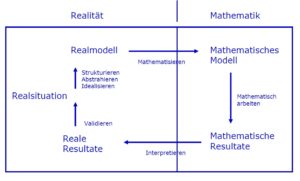
Die Gemeinsamkeit, die also alle Modellierungsaufgaben haben, ist der ihnen zugrunde liegende Prozess, über den das gegebene Problem gelöst wird, welchen Maaß in ihrer Definition von Modellierungsaufgaben schon in aller Kürze beschreibt. Gleichzeitig merkt sie an, dass jede Darstellung von Modellierung, stets selbst nur ein Modell des Ganzen sein kann und dass nur in den seltensten Fällen die skizzierten Kreislaufdarstellungen auch wirklich streng nach Art einer algorithmischen Vorgabe durchlaufen werden (vgl. Maaß 2007, S. 13). Trotzdem eignet sich das Schema des vielfach verwendeten Kreislaufs, um das Wesen der Modellierungsaufgaben zu beschreiben:
Die Ausgangslage ist eine reale Situation, die eine Problemstellung mit sich bringt. Erster Schritt im Modellierungsprozess muss sein, diese Situation in den Blick zu nehmen und Informationen zu sammeln. Sind diese Informationen zusammengetragen, gilt es ein Modell zu entwickeln, welches die Situation bestmöglich beschreibt. Je nach Komplexität der Situation kann es sein, dass nicht unmittelbar modelliert werden kann, also nicht unmittelbar der Schritt vom Problem hin zum mathematischem Modell gemacht werden kann. Stattdessen steht dann vor dem Modellierungsschritt noch eine Abstraktion, eine Strukturierung des Problems oder eine Idealisierung der Situation hin zu einem „realen Modell“. Danach kann ein weiterer Modellierungsschritt ausgeführt werden. Durch das mathematisieren der Situation erhält man ein mathematisches Modell, anhand dessen man mit mathematischen Werkzeugen nach einer Lösung des Ursprungsproblems suchen kann. Wie bei allen Aufgaben folgt in einem nächsten Schritt eine innermathematische Überprüfung dieses Ergebnisses auf Plausibilität. Ist diese erfolgreich, so ist der Prozess noch nicht zwangsläufig abgeschlossen. Zum einen ist meist eine Rückinterpretation notwendig, d.h. die Übertragung der Lösung auf das reale Modell oder die reale Situation, zum anderen muss im Rahmen dieser Rückinterpretation eine Validierung gegenüber der realen Situation vorgenommen werden. Je nach Ergebnis dieser Validierung muss ggf. an den Annahmen, die bei der Idealisierung des Problems oder bei der Modellierung des Realmodells getroffen wurden, weiter gearbeitet werden. Ein neues oder feineres Modell muss entwickelt und der Prozess, den man als Kreislauf beschreiben kann, muss mehrfach durchlaufen werden, bis die Rückinterpretation schlüssige Ergebnisse liefert. Erst dann ist der gesamte Modellierungsprozess abgeschlossen (vgl. Kaiser 1995, S. 67). Eigenschaften von Modellierungsaufgaben Modellierungsaufgaben sind von ihrem Grundsatz her immer offene Aufgaben, also Aufgabenstellungen, deren Lösungsweg nicht vorgegeben und bei denen die Lösung ggf. auch nicht eindeutig zu bestimmen ist. Offene Aufgaben können jedoch nicht gleichgesetzt werden zu Modellierungsaufgaben, da bei ihnen ggf. der Schritt vom realen Problem zum mathematischen Problem schon vollzogen ist, lediglich ohne vorzugeben mit welchem Werkzeug das Problem bearbeitet werden soll. Es lässt sich also kurz sagen, Modellierungsaufgaben sind stets:
|
 Formalisieren Formalisieren |
| Kaiser G.: Realitätsbezüge im Mathematikunterricht – Ein Überblick über die aktuelle und historische Diskussion. In: Graumann G. u.a. (Hrsg.). Materialien für einen realitätsbezogenen Mathematikunterricht Band 2. Bad Salzdetfurth ü. Hildesheim: 1995, S. 66-81.
Maaß K.: Mathematisches Modellieren – Aufgaben für die Sekundarstufe I. Berlin: Cornlsen. 2007. |
| Wir weisen darauf hin, dass die aufgelisteten Seiten nicht Teil des Didagma-Projektes sind. Daher übernehmen wir keine Haftung für die Inhalte und die Richtigkeit dieser Seiten. Falls der Link defekt, oder der Seiteninhalt unpassend sein sollte würden wir uns freuen darüber informiert zu werden.
|
| Notengebung im Modellierungsprozess |
Verantwortlich: unbekannt